В статье рассмотрены основные принципы дизайна прогрессивных очковых линз, их отличия от бифокальных и трифокальных линз. Объяснено создание поверхности зоны прогрессии, отличия линз жесткого и мягкого дизайнов.
Оптика прогрессивной поверхности
Схема на рис. 1 показывает, как средняя оптическая сила распределяется по прогрессивной поверхности линзы. Это можно продемонстрировать либо с помощью контурных линий, обозначающих среднюю рефракцию, либо через ее отличие от желаемой рефракции поверхности. На рис. 1 мы видим, как изменяется средняя оптическая сила линзы с двумя дугообразными сегментами, загнутыми вверх и вниз, такая линза была представлена ранее на рис. 5а во второй части статьи.

Рис. 1. Изменение средней оптической силы прогрессивной линзы с нулевой рефракцией для дали и добавкой для чтения +2,00 дптр
Отметим, что контуры средней оптической силы строятся на основе значений переменной M, которая считается по формуле
M = (FT + FS)/2.
Пунктирной линией обозначен меридиан прогрессивной поверхности, крест вверху в зоне для дали показывает референсную точку для дали, а внизу – для близи. Крест в центре установочный, он должен располагаться, как правило, перед центром зрачка пациента при помещении линзы в оправу. По рис. 1 заметно, что дизайн линзы мягкий, для этого проведено снижение средней оптической силы вдоль горизонтали, когда глаз поворачивается слева направо и обратно – в зоне прогрессии и зоне аддидации. Очень хорошо это видно на рис. 2, на нем показано изменение оптической силы вдоль горизонтальной линии, которая проходит через референсную точку для близи.

Рис. 2. Изменение средней оптической силы, иллюстрирующее мягкость данного дизайна с точки зрения снижения оптической силы
Графическая схема, демонстрирующая так называемую ошибку средней оптической силы, создается путем сравнения дизайн-концепта и схемы изменения средней оптической силы – так показывают, где ошибка и насколько полученная модель отличается от рефракции дизайн-концепта линзы. На рис. 3а схема изменения средней оптической силы для линзы с нулевой рефракцией для дали и добавкой для чтения +2,00 дптр, которая изображена на рис. 1, наложена на дизайн-концепт мультифокальной линзы с верхней и нижней дугообразными зонами (см. рис. 5а во второй части статьи), обозначенный пунктирными линиями. Интервал между зонами был снижен на 0,5 дптр для упрощения восприятия наложения двух схем.
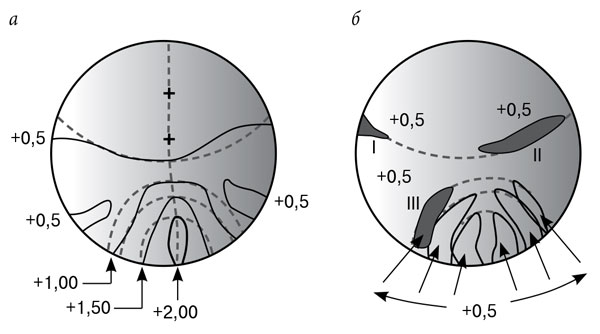
Рис. 3. Изображение ошибки средней оптической силы для линзы с нулевой рефракцией для дали и добавкой для чтения +2,00 дптр:
а – схема средней оптической силы для линзы с дизайном «дуга вверх и дуга вниз»; б – схема ошибки средней оптической силы для этого дизайна
Информацию, которую нам дает схема ошибки средней рефракции (рис. 3б), получают следующим способом. В зоне I рефракция, предполагаемая дизайн-концептом линзы, составляет +0,5 дптр (см. рис. 5а*), но средняя оптическая сила еще не подошла к этому значению, поэтому величина ошибки составляет –0,5 дптр. В зоне II, согласно дизайн-концепту, у нас должна быть нулевая оптическая сила, в то время как на самом деле она выросла до +0,5 дптр, именно такое значение принимает ошибка средней рефракции. Точно так же для зоны III требуется оптическая сила +1,0 дптр, но по факту она +0,5 дптр, поэтому ошибка равна –0,5 дптр. Понятно, что каждая похожая на клык зона рядом с зоной для близи на полдиоптрии слабее по отношению к дизайн-концепту.
Помимо асимметричного астигматизма, свойственного линзам с зоной прогрессии, им присущи и наклонные искажения, которые возникают следующим образом. Представим, что глаз смотрит на три вертикальные линии сквозь бифокальную линзу, которую держат на расстоянии вытянутой руки, у этой линзы сегмент с плоской верхней границей, у него нулевая оптическая сила вдаль и сила сегмента для близи +2,0 дптр. Поскольку в нижнем сегменте для близи оптическая сила выше, в нем сильнее и оптическое увеличение, так что воспринимаемый вид трех линий будет таким, как показано на рис. 4а. Правда, благодаря неизменности добавки для чтения по всей зоне для близи, увеличение тоже не меняется, так что три линии будут видны как вертикальные.
Теперь посмотрим, что будет при рассматривании этих вертикальных параллельных линий через прогрессивную поверхность (рис. 4б). В зоне прогрессии оптическая сила поверхности растет по мере продвижения от зоны для дали к зоне для близи, а это ведет к росту оптического увеличения. Очевидно, что не бывает роста рефракции без роста этого увеличения.
Таким образом, из-за изменения увеличения вертикальные линии будут видны как наклонные. Такое действие меняющегося увеличения часто отмечают новички, которые в первый раз надели очки с прогрессивными линзами – им кажется, что они «поплыли».
К счастью, наклонные искажения вертикальных линий можно минимизировать, для этого намеренно снижают оптическую силу и, соответственно, увеличение на краях зоны прогрессии, так что благодаря пластичности зрительной системы человека эффект плавания скоро исчезает. Из схемы средней оптической силы на рис. 2 можно понять, что именно это и делают в типичных современных прогрессивных линзах. В результате добиваются эффекта, изображенного на рис. 4в.

Рис. 4. Наклонные искажения в прогрессивной линзе:
а – вид вертикальных линий через бифокальную линзу; б – вид вертикальных линий через прогрессивную линзу: в – снижение наклонных искажений путем уменьшения оптической силы
Призменное утончение
На рис. 5а, представленном в этой статье и иллюстрирующем поперечный разрез прогрессивной линзы, видно, что толщина линзы на краю выше вверху. Это объясняется тем, что кривизна поверхности растет книзу линзы на величину, равную добавке для чтения. В результате толщина в центре у положительной линзы выходит больше, чем если бы это требовалось лишь оптической силой для дали. Для того чтобы выровнять толщину линзы вверху и внизу, можно применить призматический компонент с основанием вниз.

Рис. 5. Призменное утончение:
а – прогрессивная линза без призменного утончения; б – удаление призмы с основанием вверх для уравнения размеров краев; в – прогрессивная линза с призменным утончением
Благодаря использованию такой призмы, уменьшающей толщину (призменное утончение), толстый слой в центре линзы уменьшается. Одинаковое призменное утончение вносится в каждую линзу. Как правило, значение призмы составляет две третьих от добавки для чтения. Например, для добавки для чтения +1,50 дптр используется призма 1 прдптр, для добавки +2,00 дптр – 1,33 прдптр. Поскольку величина этих призм очень маленькая, на зрительное восприятие они практически не влияют.
При проверке параметров прогрессивной линзы нужно учитывать этот призматический компонент, если он присутствует. Призму обычно проверяют в геометрическом центре линзы, в случае отсутствия корригирующего призматического элемента, данные покажут только призматическое утончение. Если же и его нет, то оптический центр будет совпадать с геометрическим центром линзы.
Для того чтобы решить, использовать ли призменное утончение или нет, рассматривают оптическую силу и форму готовой линзы. Например, при сочетании неглубокой формы линзы с малой глубиной зоны прогрессии в необработанной заготовке геометрический центр будет смещен к нижнему краю линзы, так что применение призменного утончения не окажет влияния на толщину (рис. 6). Также многие лаборатории не используют призменное утончение в линзах с большой отрицательной рефракцией.

Рис. 6. Линза с неглубокой формой без призменного утончения
Призматический эффект в зоне прогрессии
Рис. 7 показывает ход луча, падающего в точке D на меридиане прогрессивной линзы, находящейся на расстоянии у см ниже референсной точки призмы A1.

Рис. 7. Призматический эффект по меридианной линии прогрессивной линзы
Считается, что оптический центр зоны для дали находится в этой точке (то есть призменное утончение не используется). Наклон падающего луча обозначен u, и нам известно значение оптической силы в точке D – она равняется FT. Это значение можно получить из знания функции оптической силы вдоль поверхности (степенной закон), изображенной на рис. 3*, либо считать со схемы изменения средней оптической силы. В точке D луч испытывает преломление и дальше идет под углом u´ к оси. Отклонение луча P, выраженное в призменных диоптриях (прдптр), есть u´ – u.
Из определения призменной диоптрии следует:
u = 100 y / l = y L (l выражено в сантиметрах),
u´ = 100 y / l´ = y L´ (l´ выражено в сантиметрах), так что P = u´ – u = y (L´ – L) = y FT.
Это, конечно же, правило Прентиса. Вывод предполагает использование параксиальной теории, которая дает хорошее приближение к истинному отклонению касательного луча в точке падения. Если меридиональная линия представляет собой умбилическую линию (так что FT = FS), то призматический эффект просто равен P = y F, где F – мгновенная оптическая сила поверхности в рассматриваемой точке, судя по графику, который демонстрирует степенной закон для рассматриваемой поверхности, как видно из рис. 2б и 3.
По сравнению с бифокальным и трифокальным дизайнами прогрессивные линзы обладают четырьмя важными преимуществами. Во-первых, они обеспечивают непрерывный обзор от дальней точки до ближней без пропусков в пределах видимости (рис. 8).

Рис. 8. Сравнение усилия аккомодации в трифокальной (вверху) и прогрессивной (внизу) линзах![]() – четкое зрение;
– четкое зрение; ![]() – размытое зрение
– размытое зрение
Во-вторых, пациент использует в таких линзах оставшуюся аккомодацию более естественным образом, поскольку усилие аккомодации в них растет постепенно. Это свойство продемонстрировано на рис. 8, в котором показано усилие аккомодации у пациента с ее амплитудой, равной 1,00 дптр, который носит либо трифокальные, либо прогрессивные линзы. Обратите внимание на флуктуации в аккомодации у пользователя трифокальных линз, которые пропадают при переходе на прогрессивные линзы.
В-третьих, в прогрессивных линзах нет скачка при переходе от зоны к зоне. В-четвертых, на прогрессивной линзе нет разделительной линии между сегментами – выглядит она, как однофокальная линза.
Автор:
Мо Джали (Mo Jalie), приглашенный профессор кафедры оптометрии Ольстерского университета (Колрейн, Ирландия)
Перевод: И. В. Ластовская
Оригинал статьи опубликован в журнале Optician 13.09.2016 г. Перевод печатается с разрешения редакции
© РА «Веко»
Печатная версия статьи опубликована в журнале «Современная оптометрия» [2021. № 4 (143)].
По вопросам приобретения журналов и оформления подписки обращайтесь в отдел продаж РА «Веко»:
- Тел.: (812) 603-40-02.
- E-mail: magazine@veko.ru
- veko.ru
Наши страницы в соцсетях: